Alloy 6: it's about Time
Alloy is a powerful formal specification language, but it’s historically been weak at modeling concurrency. AWS raised this as a critical issue for why they went with TLA+. Alloy writers built a lot of tricks to emulate time, but it can feel like you’re working against the language.
Alloy 6 aims to change that with built-in temporal operators. Right now it’s poorly documented, and since I maintain the alloydocs, I sat down and figured it all out.
This is not comprehensive and I’m not covering all the semantics or all of the new operators, just enough to give you a sense of what we now have. Also, this assumes you’re already familiar with Alloy. If this is your first time hearing of it, I have a gentler introduction here.
Example
We’ll start with a simple temporal system. We have a graph of nodes and edges, and a single ball on one of the nodes. Every step the ball can move to a connected node.
Note: we haven’t yet gotten the pygments lexer updated, so until that’s merged the syntax highlighting is gonna be a bit wonky. Sorry!
sig Node {
edges: set Node
}
fact "Connected graph" {
some n: Node | n.*edges = Node
}
fact "No self edges" {
no iden & edges
}
one sig Ball {
-- note the var
var loc: Node
}
The only new thing so far is the var loc, which says the loc relation is mutable. Like most specification languages, Alloy divides time into a series of discrete steps, where for each step loc' is the value in the next step. We can make both relations and top-level signatures mutable, like var sig Node. In that case, Node would be the set of all nodes in the current step and Node' the set of all nodes in the next step.
Now let’s add a way to model the ball moving between nodes:
pred move[b: Ball, n: Node] {
n in b.loc.edges
b.loc' = n
}
This predicate is true if there’s an edge from the current node to n and, in the next step, the ball is in n— it moved from the current location. I can use this predicate as part of another predicate, like this:
pred moved[b: Ball] {
some n: Node | move[b, n]
}
pred unchanged[b: Ball] {
b.loc = b.loc'
}
Let’s look for an alloy instance where moved is true on every step, ie the ball moves through the graph.
example1: run {
some b: Ball |
always moved[b]
}
The always keyword is new. always f means that for all future states–
Okay editorial sidenote, it always annoyed me that temporal logics use “future” to mean “current or later steps.” Like I get the value of including the present state, but it confuses people who are used to the everyday meaning. So I’m going to define future⁺ as “future explicitly including the current state” and future⁻ as “explicitly excluding current state”.1
–always f means that for all future⁺ states, f is true. So always moved[b] means that between any two steps, the ball moves. Simple. Now we can run it like any other alloy predicate:
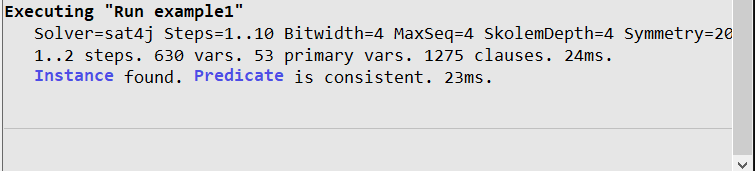
By default, the analyzer looks for traces up to 10 steps long. You can change the number of maximum steps with for $max steps and the minimum with for $min..$max steps. Anyway, let’s look at a model:
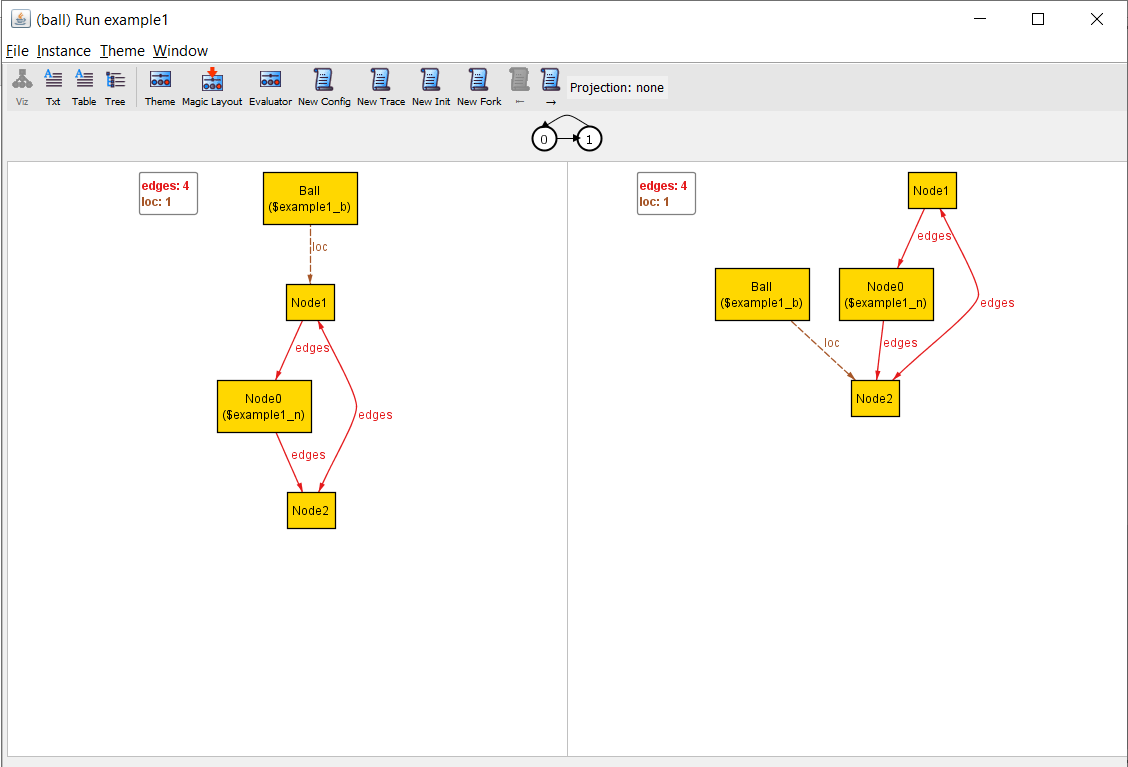
This is different!
The new visualizer
Let’s do a quick breakdown.
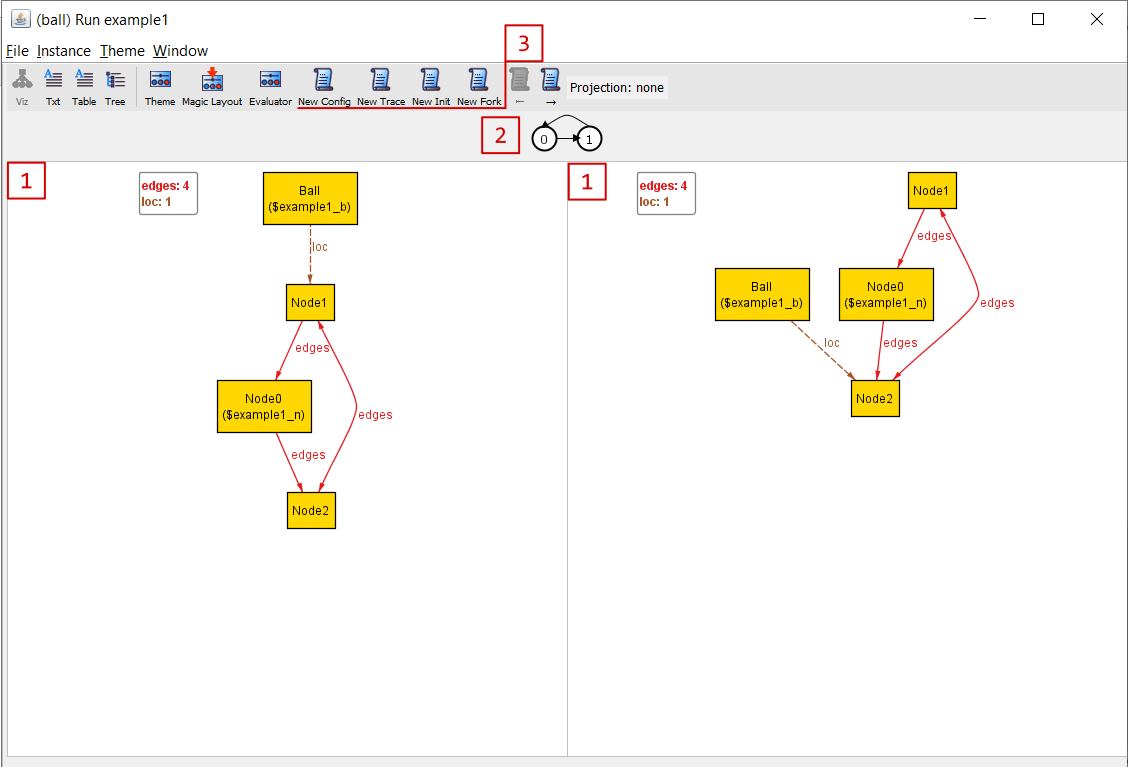
- The visualizer shows step-pairs, this state and the next. The evaluator is based on the current step, as are things like
univandiden. There’s no way to see the entire behavior at once. - All traces are lassos: a sequence of states that either terminates or loops back to a previous state. Since all Alloy scopes are finite, all traces are guaranteed to be lassos, though it could be too big to fit in memory! The two states we currently looking at are highlighted in white, any other state will be in grey.
Instead of having “next instance”, we have four options:
- “New Config” changes the immutable parts of the model and finds a new behavior trace. In this case, it would give us an entirely new graph topology
- “New Init” fixes the immutable relations and finds a new initial state and behavior trace. We’d have the same topology, but the ball would start on a different node.
- “New Trace” finds a new behavior trace from the existing configuration and initial state. So the ball would still start on
Node1, but it would move toNode0instead ofNode2. - “New Fork” can only be used in the middle of a trace. It fixes the present state (and states before) and finds a new next state.
(One footgun here: like with “New Instance”, finding a new Model will show a popup if there are no new solutions. This hides the visualizer behind the editor but does not close it. In fact you can still work with it: even if you run out of forks you can generate a new config, etc.)
The visualizer layout isn’t stable. Nodes can be laid out differently in successive steps, which makes it harder to read what’s actually happening. I’m hoping this can be fixed in a later update.
If your model is entirely static, it shows the old visualizer with a “New Instance” button.
Other future-time operators
Alloy’s always comes from Linear Temporal Logic (LTL). There’s also eventually p, which says that p is true in at least one future⁺ state. Most speclangs use eventually to express liveness properties, aka “does something good always happen in all traces”. This is where Alloy’s model-finder comes in handy: we can find example traces where something eventually happens, even if it’s not a guaranteed liveness property. This next snippet gives us models where we eventually reach all nodes:
example2: run {
some b: Ball {
always moved[b]
all n: Node |
eventually b.loc = n
}
}
Another operator we have is after p, which says p is true in the next state. Here’s how we can find traces where we move from a node and immediately move back:
example3: run {
some b: Ball {
always moved[b]
eventually some n: Node {
b.loc = n
after after (b.loc = n)
-- or `after (b.loc' = n)`
}
}
}
Let’s make things more interesting:
one sig Final in Node {}
How can we say “the ball doesn’t reach Final unless it’s been to all other nodes first?” To do this we use the binary operator until:
all n: Node - Final |
b.loc != Final until b.loc = n
There’s a tricky subtlety to until. F until G means that F is true at least until G is true… but it also guarantees G! In other words, it’s identical to (F until G) and (eventually G). The “weaker” version is G releases F: either G is true before F is false, or G never happens and F is always true. Niehter of these guarantee F is ever false, just that it’s not false before G is true.
It’s a little unintuitive to define our property this way: we’ve specified “we can’t reach Final until we’ve reached Node1 AND we can’t reach Final until we’ve reached Node2 AND …” It’d make more sense to say “we can’t reach Final until we’ve reached Node1 AND Node2 AND …” You might try to write that as
b.loc != Final until
all n: Node - Final |
b.loc = n
But this says that we don’t reach Final until b.loc is all other nodes in the same step. Since b.loc can only be one Node at a time, this can only be true if the graph has two or fewer nodes!
There’s a better way to simplify our property, using:
Past-time operators
Every future operator in Alloy has a corresponding past operator.
| future | past |
|---|---|
| after | before |
| always | historically |
| eventually | once |
| until | since |
| releases | triggered |
(The one exception is `a ; b`, which is equivalent to `a and after b`.)
Here’s a predicate for “have we ever been at a node”:
pred reached[b: Ball, n: Node] {
once b.loc = n
}
We can use reached to determine behavior, such as by having the ball prioritize new nodes before reached ones. We can also use it to express properties, like “we don’t go to Final until we’ve reached all other nodes”:
(b.loc != Final) until (all n: Node - Final | b.reached[n])
Aside: Temporal Logic is Confusing
I realize this might be intimidating if you aren’t elbow-deep in temporal logic. Think of each temporal operator as a scope. All mutable values and nested temporal operators are relative to that scope. This means that loc and after loc are two different “loc“s. Conventionally, a predicate outside any temporal operators refers to the first state.
This gets more confusing when you have multiple levels. Given var x: Int and the statement
eventually {
before (x = 1)
x = 2
after (x = 3)
after after (x = 4)
}
This is a trace that satisfies it:
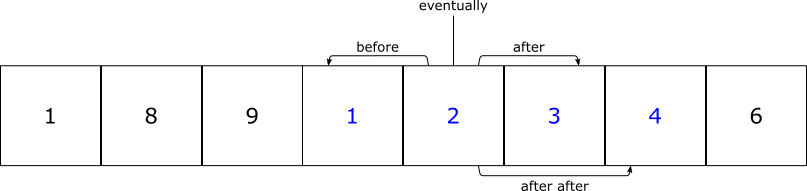
The before and afters are all relative to the step where x = 2. It’s all a little hairy, but you get used to it pretty quickly.
You can’t “move” values between operators, except through `'`. If you need to use the last step’s value in the current step, you need to pull the value into a quantifier:
some n: Int {
before (val = n)
f[n]
}
(Clever people might notice before f[n'], but using a quantifier is more general.)
Temporal logic is notoriously tricky to reason through. What’s the difference between always eventually x and eventually always x? We can use Alloy to give us an example where the first is true but not the second:
var lone sig N {}
run {
(always eventually some N) and not
(eventually always some N)
}
The first predicate says that some N always is true at some point in the future, while the second predicate says that some N becomes permanently true. If we switch the order of the two clauses, Alloy will not find any instances, meaning the second predicate is strictly more powerful.
Don’t worry if you have some trouble with this, it’s just something that comes with practice.
Doing a Concurrency
Now that we have all the parts, let’s add in concurrency.
- one sig Ball {
+ sig Ball {
We can allow only one ball to move each step, or let them move simultaneously. We’ll start with the former case:
pred step {
some b: Ball {
some n: Node | move[b, n]
all b": Ball - b | unchanged[b"]
}
}
pred spec {
always step
}
We have to not just say that one ball moves, but that the others stay in place. This is called fully determining the next state. If we don’t do that, Alloy can choose an arbitrary value for b".loc'.2
Now let’s add a property to check, such as two balls are never on the same node at the same time:
pred no_overlap {
spec => always {
no disj b, b": Ball | b.loc = b".loc
}
}
check {no_overlap} for 5 but exactly 2 Ball
This fails:
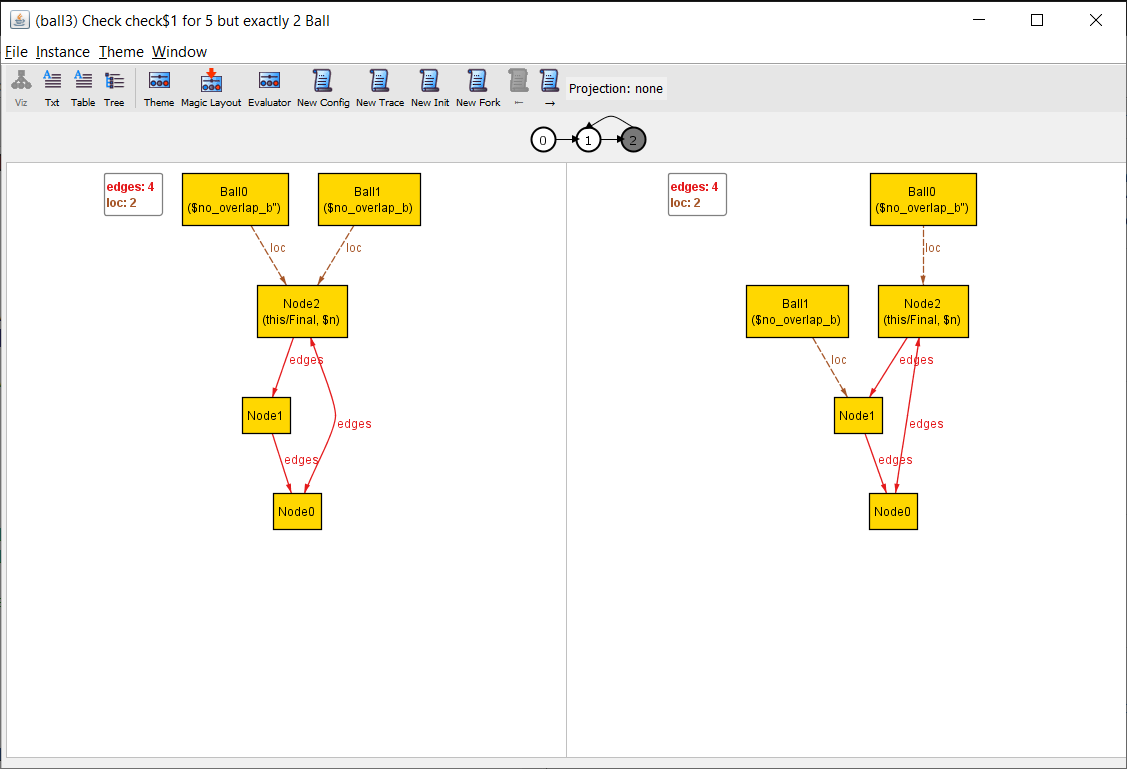
Oops, forgot to say they have to start in different states!
pred spec {
+ all disj b, b": Ball {
+ b.loc != b".loc
+ }
always step
}
The all disj is outside any temporal operators. That means it applies to only the first state.
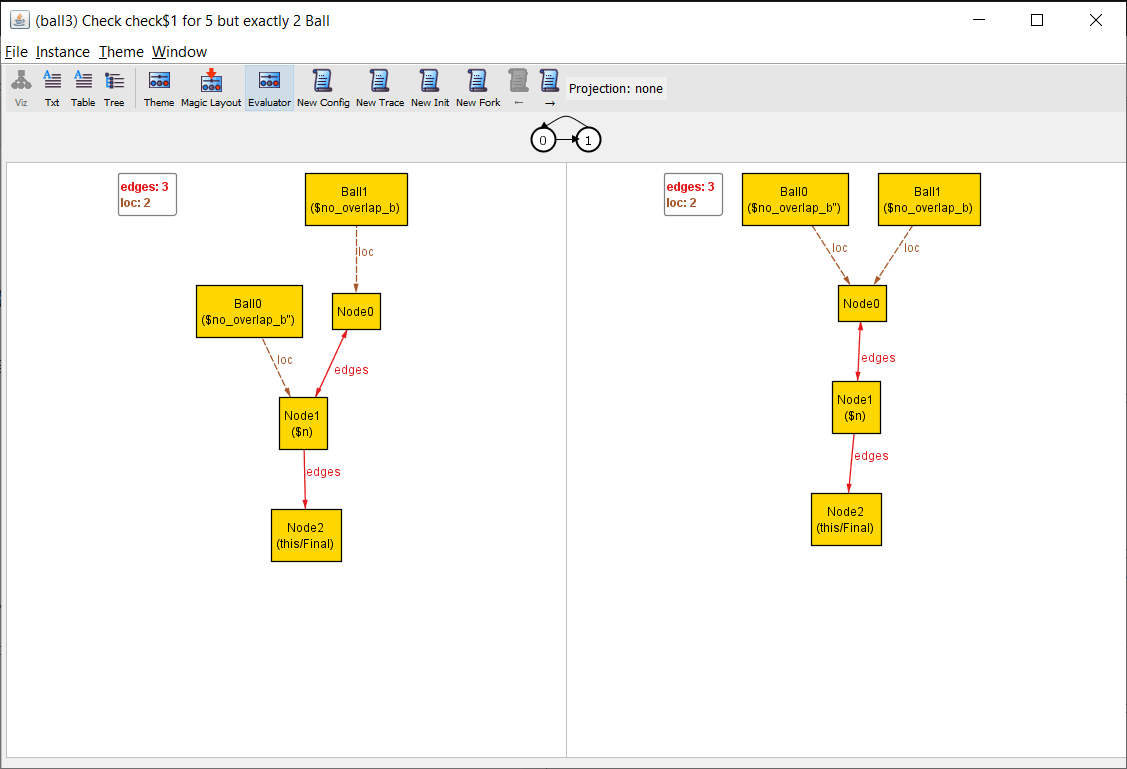
That’s better. We can fix this by only letting a ball move into an “empty” node:
pred move[b: Ball, n: Node] {
n in b.loc.edges
+ no b": Ball | b".loc = n
b.loc' = n
}
Alloy no longer finds a counterexample. So let’s change the spec to allow all balls to move simultaneously:
pred step {
- some b: Ball {
- some n: Node | move[b, n]
- all b": Ball - b | unchanged[b"]
- }
+ all b: Ball | moved[b] or unchanged[b]
}
Now we get a new counterexample!
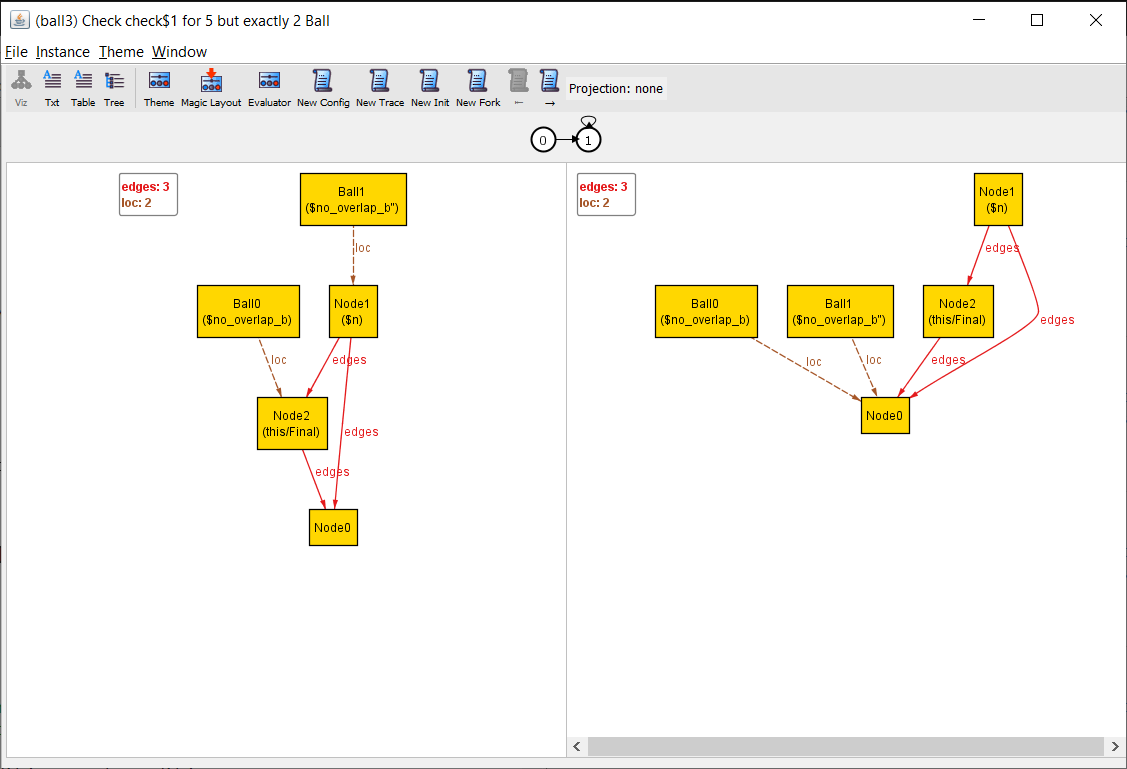
Each Ball checks that it’s not moving into another Ball’s location, so they both pick the same third node and move into it simultaneously. Modeling these kinds of systems used to be very challenging in legacy Alloy, and I’m glad it’s so much easier now.
Final spec:
show spec
sig Node {
edges: set Node
}
one sig Final in Node {}
fact "Connected graph" {
some n: Node | n.*edges = Node
}
fact "No self edges" {
no iden & edges
}
sig Ball {
var loc: Node
}
pred move[b: Ball, n: Node] {
n in b.loc.edges
no b": Ball | b".loc = n
b.loc' = n
}
pred moved[b: Ball] {
some n: Node | move[b, n]
}
pred unchanged[b: Ball] {
b.loc = b.loc'
}
pred reached[b: Ball, n: Node] {
once b.loc = n
}
pred step {
all b: Ball | moved[b] or unchanged[b]
}
pred spec {
all disj b, b": Ball {
b.loc != b".loc
}
always step
}
pred no_overlap {
spec => always {
no disj b, b": Ball | b.loc = b".loc
}
}
check {no_overlap} for 5 but exactly 2 Ball
Thoughts
I’m really excited about this update! Alloy is now “the right tool for the job” in a lot more situations than it used to be. There’s still some rough edges to polish, but that’s always the case with these kinds of tools. The bigger “problem” is that Alloy 6 is too powerful: the temporal operators effectively obsolete most of the existing learning material. There’s no need to do tricky shenanigans with time sigs and dynamic multirelations when the new semantics are simpler and stronger. So now we need to make new documentation, tutorials, and examples. The Alloy 6 developers are writing a new book, and I’ve got a bunch of work to do, too.
I also have to throw out my entire draft on “TLA+ vs Alloy” and start over. Go figure.
If you’re interested in learning more about Alloy, I maintain the Alloydocs, which I’m in the process of updating. I also provide consulting and training, though I’ll need a bit of time to redesign my workshop.
Thanks to Lorin Hochstein, Jay Parlar, and Daniel Jackson for feedback. I have a weekly newsletter where I announce new blog posts and write additional essays. If you enjoyed this, why not subscribe?
- I am absolutely certain that someone else has come up with the same convention, except the other way around. Someone I asked for feedback made this exact mistake. [return]
- TLA+ raises an error if the next state isn’t fully specified. I’d like to see Alloy raise a warning, but there’s technical issues with that. [return]