Let's Prove Leftpad

Someone recently told me a project isn’t real until you do a retrospective, so I think it’s time to do one for Let’s Prove Leftpad. Short explanation: it’s a repository of proofs of leftpad, in different proof systems.

Long explanation: the rest of this post.

Background

I’m into formal methods, the discipline of proving software correct. Consider the following contrived code:

def add(x: int, y: int): int {
  if(x == 12976 && y == 14867) {
    return x - y;
  }
  return x + y;
}

This typechecks, and any black-box unit test would find that add(x, y) == x + y. It would also pass property testing: if you randomly picked two 16 bit integers, you’d have to run something like 500 million tests to have a 10% chance of triggering the bug. A formal verification tool would fail the code 100% of the time, and pass it if only if it was always correct.

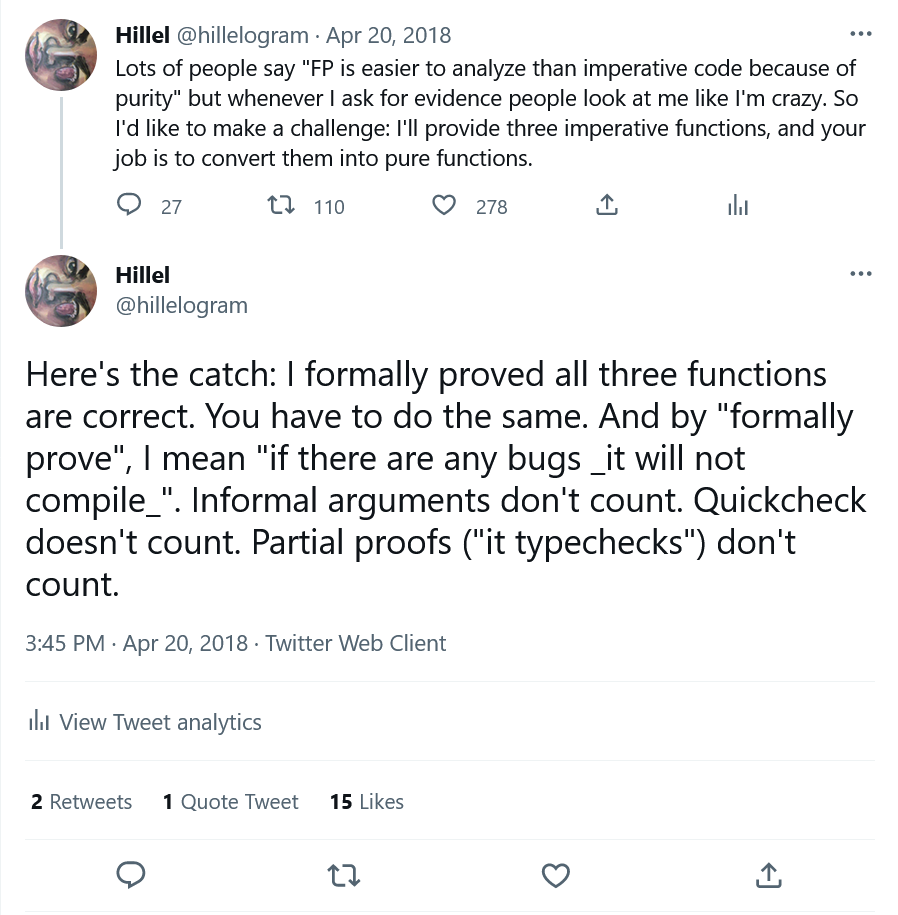
The tradeoff for this kind of power is difficulty: proving code correct is very, very hard to do. This is pretty widely accepted in the FM discipline. Outsiders, though, often assume that function programs are easier to prove correct that imperative programs. While this might be true for informal reasoning, it’s not that true for formal proof. To show this, in 2018 I made an online challenge to people:

I provided two warmups, leftpad and unique, and a main challenge, called “fulcrum”. The full details and results are documented here.

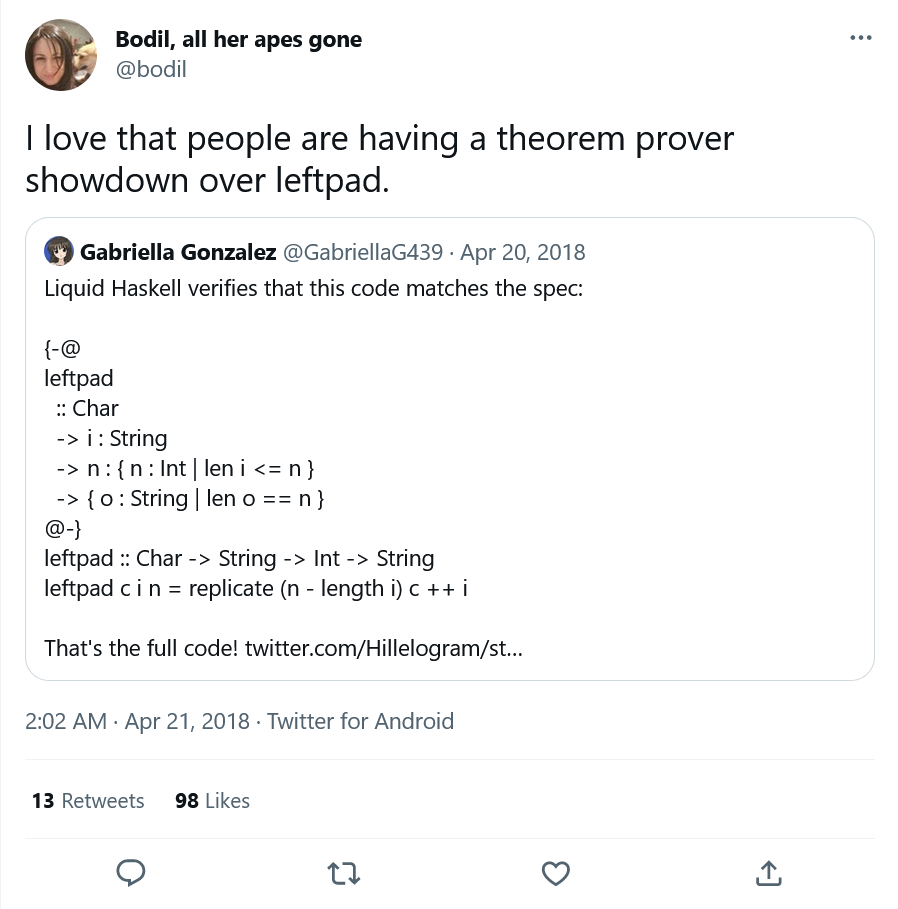
Two things came out of the theorem showdown. First, it put me in touch with Lars Hupel, and we’ve been fast friends ever since. Second, this tweet:

And that’s when I realized that leftpad is a great proving exercise.

On Leftpad

For those of you who weren’t around in 2016, leftpad does this:

>> leftpad('!', 5, "foo")
!!foo
>> leftpad('!', 2, "foo")
foo

Six years ago a leftpad NPM package broke the whole internet. I put it in for the meme value and was surprised when it turned out to be such a good problem. That’s because it has a simple implementation and a complex spec:

1. The length of the output is max(n, len(str))
2. The prefix of the output is padding characters and nothing but padding characters
3. The suffix of the output is the original string.

So it’s enough to show the differences between proof approaches without being too difficult to actually prove. For example, let’s compare Dafny and Lean. Here’s the Dafny:

 1function method max(a: int, b: int): int
 2{
 3    if a > b then a else b
 4}
 5
 6method LeftPad(c: char, n: int, s: seq<char>) returns (v: seq<char>)
 7ensures |v| == max(n, |s|)
 8ensures forall i :: 0 <= i < n - |s| ==> v[i] == c
 9ensures forall i :: 0 <= i < |s| ==> v[max(n - |s|, 0)+i] == s[i]
10{
11    
12    var pad, i := max(n - |s|, 0), 0;
13    v := s;
14    while i < pad decreases pad - i
15    invariant 0 <= i <= pad
16    invariant |v| == |s| + i
17    invariant forall j :: 0 <= j < i ==> v[j] == c
18    invariant forall j :: 0 <= j < |s| ==> v[i+j] == s[j]
19    {
20        v := [c] + v;
21        i := i + 1;
22    }
23}
24
25method Main() {
26    var l1 := LeftPad('0', 5, "foo");
27    var l2 := LeftPad('0', 1, "foo");
28    print l1 + "\n\n";
29    print l2;
30}

Dafny is for writing contained verified modules as part of larger production codebases. It compiles to C#, Java, and JavaScript. The implementation language looks like a “normal program”. If you strip out all the verification stuff you’d end up with a straightforward appending while loop.

The leftpad properties are specified via ensures postconditions on the method. Dafny then shells out to a theorem prover (default Z3) to do the hard work of verification. In the perfect world, the user wouldn’t have to do anything else. In practice the prover can’t automatically infer everything, so we need to provide intermediate properties as stepping stones. Instead of directly proving the ensures from the code, the prover instead proves the while loop invariants from the code, and then the ensures from the invariants. And that’s how we get leftpad!

Now compare it to the Lean:¹

 1import data.nat.basic
 2import data.list
 3open list
 4
 5universes u
 6variables {α : Type u}
 7
 8def leftpad (n : ℕ) (a : α) (l : list α) : list α :=
 9repeat a (n - length l) ++ l
10
11#eval list.as_string (leftpad 5 'b' (string.to_list "ac"))
12
13theorem leftpad_length (n : ℕ) (a : α) (l : list α) : 
14length (leftpad n a l) = max n (length l) :=
15begin
16  rw leftpad, simp,
17  rw [add_comm, nat.sub_add_eq_max]
18end
19
20theorem leftpad_prefix [decidable_eq α] (n : ℕ) (a : α) (l : list α) :
21(repeat a (n - length l)) <+: (leftpad n a l) := by {rw leftpad, simp}
22
23theorem leftpad_suffix [decidable_eq α] (n : ℕ) (a : α) (l : list α) :
24l <:+ (leftpad n a l) := by {rw leftpad, simp}

Totally different! Lean is designed, first and foremost, to formalize mathematics. While Dafny is a programming language that uses a prover, Lean is a theorem prover, pure and simple. So proving things means providing steps, or “tactics”, that lead to your theorem being shown correct.

To explain the proof of leftpad_length: First we replace the leftpad invocation on line (14) with the leftpad definition: that’s what’s meant by the simp (simplify) step (16). Then we apply the add_comm (17), or “addition is commutative” theorem, to rewrite the goal as n - l + l = max n l. Finally, the nat.sub_add_eq_max theorem states that if l > n, n - l = 0 (since they’re both natural numbers), and so n - l + l = l. This completes the proof.

…So two implementations of leftpad, with identical behavior, but very different approaches to proving correctness. And when things are comparable in an interesting way, that makes me want to collect them all in one place, and so I made a repo.

Let’s Prove Leftpad

After the showdown, I reached out to everyone who did a (successful) LP proof. I asked them to provide:

1. A description of the formal methods tool they used, along with setup instructions
2. A description of how their leftpad proof is structured

The goal is to make it reasonably possible for an interested onlooker to compare the different methods and understand why they’re different. In practice, some explanations are more complete than others— Liquid Haskell has an entire blog post while Java is just a few lines. Still, most of them do a good job explaining how they work.

We currently have 22 proofs for 20 systems.² Some interesting things in no particular order:

• Proof languages generally fall into one of three categories. First, dedicated theorem provers like Lean and Agda. Second, programming languages designed to be verified, like Dafny and F*. Finally, tools to verify code in existing languages, so that you can prove code in C, Common Lisp, or Java. All of these have different use cases and different design constraints.
• The proofs for Liquid Haskell and SPARK were submitted by core developers of those projects.
• Some FM languages come with a large standard library and that makes a big difference to proof length.
• The most exotic language? Probably the verilog proof.
• The saddest thing was when I had to revert a proof in Python after the author clarified it didn’t actually prove anything, it just did property testing. I like it when people submit really surprisingly languages.

Languages we need

There’s a bunch of languages we’re still missing:

• ATS
• mCRL2
• Event-B
• CakeML
• Whiley
• Lots that are verification packages for a specific language, like Autoproof. Notably, we don’t have any proofs in array or logic programming languages.

If you know one of these, please submit a proof!

Overall this was a fun project and I hope it’s eventually useful to someone. My dream is that this eventually gets cited in an academic paper. That’d be dope.

Thanks to Predrag Gruevski and Lars Hupel for feedback. I also have a newsletter where I post weekly short essays!