Safety and Liveness Properties

Sounds like I should write a post on safety and liveness!

First, some definitions. A system is anything that has changing state. This is an incredibly broad definition that covers a wide variety of situations, like:

• Two threads in a thread scheduler
• Five servers behind a load balancer
• A reader and writer communicating on a FIFO queue
• A business workflow being manually followed
• A person waiting for the bus
• Etc.

Each system has a set of behaviors, each behavior being a possible timeline of events and states. The system also has properties we want to be true. A correct system, then, is one where every behavior preserves every property.

Consider, for example, this toy model of a system:

x = 0
while True:
  if rand() >= 0.5:
    x = (x - 1) % 3
  else:
    x = (x + 1) % 3

While this system has only three states,¹ there’s an infinite number of different behaviors: 0 → 1 → 2 → 0..., 0 → 2 → 0 → 2..., 0 → 1 → 2 → 1 → 0..., etc. Some properties of this system are “x is always in {0, 1, 2}”, “x is never the same value after each loop cycle”, and “the algorithm never terminates”.

Most software engineers don’t think about systems this way. It’s mostly used by computer scientists who are interested in formal methods, finding ways to automatically verify properties on abstract representations of the system. But you can also use this model to guide design decisions and come up with tests. If you have a property, you want high confidence that it’s actually satisfied, and having a language to talk about them makes thinking about them easier.

The most common properties are safety and liveness.

Safety

Safety properties are “bad things don’t happen”. Most people are tacitly familiar with safety properties. Some are:

• Two threads can’t both be in a critical section at the same time.
• Users cannot write to files they don’t have access to.
• We never use more than 500 kb of RAM.
• The user_id key in the table is unique.
• We never add a string to an integer.

These are all safety properties called invariants. Invariants hold over every state of the system. If there is one state in one behavior where a user can access a forbidden resource, the safety invariant is violated.

Not all safety properties are invariants. Safety properties can also be on sequences of states:

• The light cannot go straight from green to red. This is a property on pairs of states. In TLA+ they are called action properties.
• If a user makes a modification to the data and then undoes it, it’s like they never made the modification. This property involves two state transitions, so it’s a property over three states.
• Every message is received at most once by each client. This is a property on the entire behavior, since it can be broken by two states twenty steps apart.

Formally speaking, safety properties are properties with finite-length counterexamples. There is a sequence of things you can do, after which point the property is definitely broken.

As a rule, the more states involved in your safety property, the harder it is to formally verify. This means that invariants are much easier to verify than generalized-behavior proprties. So a common FM technique is to transform general properties into invariants. Take the property “x never changes to a value it’s been before.” We can turn this into an invariant by adding a history state that accumulates all changes to x, and then adding the invariant x not in history.

In this example, history is sometimes called an auxiliary variable. It’s added to help with the verification but isn’t part of the physical system.²

Liveness

If safety is “bad things don’t happen”, then liveness is “good things do happen”.

• Every message is received at least once by each client.

No finite sequence of steps can break this property. Even if the message isn’t delivered now, it might be delivered in the future. The only way to break a liveness property is to show that at no point in the future does it ever become true.

In practice, specifications have “implicit timescales”. If I’m trying to meet up with a friend for brunch, it’s not okay if they receive the message ten days from now. So we can consider “X doesn’t happen” to also include “X happens well outside our time bound” and treat both failure modes as liveness violations.

Unsurprisingly, liveness properties are significantly more complex than safety properties. There are three kinds of common liveness counterexamples:

1. The system has an infinite chain of distinct states that don’t ever satisfy the liveness. For example, the code x=0; while true {x--;} will never have the property “eventually x = 1”.
2. The system reaches a point where it can’t make progress. This could be a crash, a deadlock, or running to completion without satisfying the property.
3. There’s a way for a behavior to return to a previous state. Then we can we cycle between a small state of sets endlessly. In state graphs, this looks like a line of states followed by a loop, leading to the nickname “lassos”.

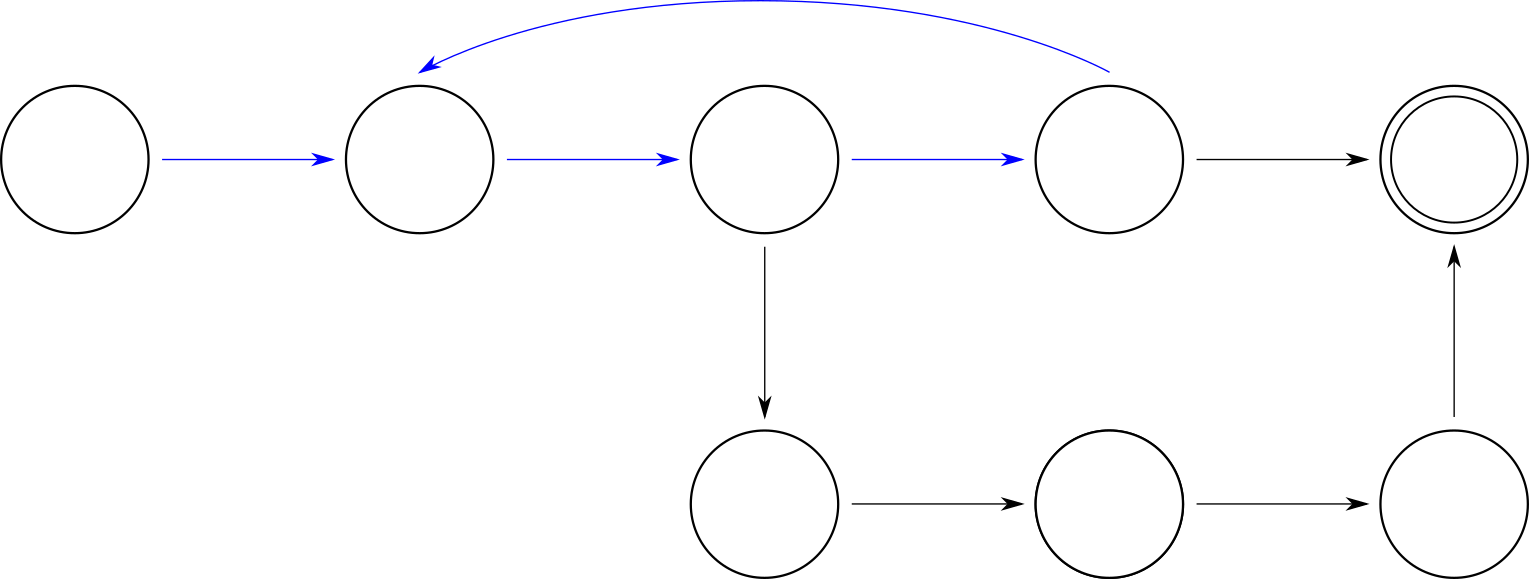
Formally verifying type (1) properties is extremely difficult and often requires lots of manual labour. In practice, most automatic model checkers focus on lassos, as they can be checked over a finite state space. Lassos also cover failures of type (2), where a “crash” is a behavior with a single-state lasso.

Some more liveness properties:

• Each thread eventually is in the critical section.
• The database is eventually consistent.
• Every HTTP request is eventually closed.
• Deleting an event in a calendar app also removes it from all other synced devices.
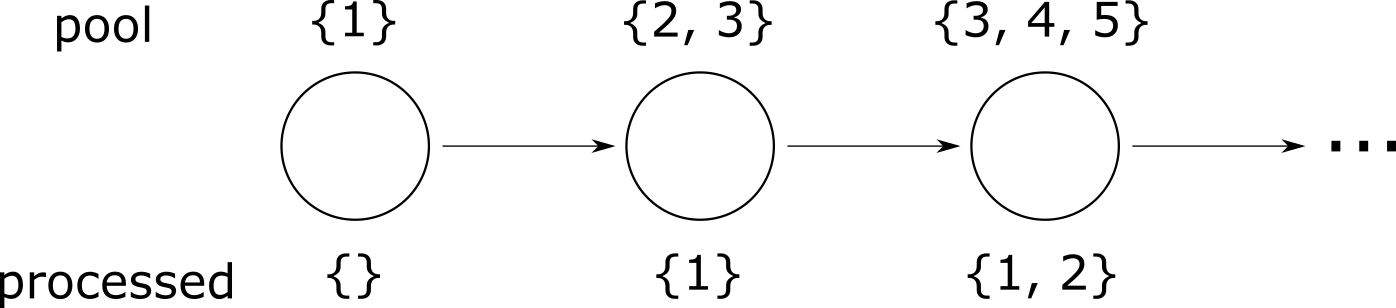
• TASK1: Every task that enters the task pool is eventually processed by a worker.
• TASK2: Eventually all of the tasks are processed by workers.

While they look similar, TASK1 and TASK2 are different liveness properties. For TASK2 to be true, there has to be a point where there are no tasks remaining. If tasks are coming in faster than they can be processed, TASK1 can hold even if TASK2 doesn’t. This is the benefit of specifying properties: you’re expressing precisely what you want out of your system, and so can distinguish a correct system from an almost-correct-but-not-exactly system.

Liveness properties can get significantly more complex:

• While a version bump may put different servers on different versions, eventually all servers will be on the same version, whether the upgrade or a rollback.
• The counter is generally monotonic: while it may bounce around a bit, over a long enough time it increments more often than it decrements.³

A particularly common type of liveness requirement is fairness. A very high level, fairness requirements are “things that can happen will happen.” Consider a LIFO thread scheduler, which always wakes the most recent thread that went to sleep. If ten threads go to sleep at the same time, the first thread might never be reached, as the scheduler will always prioritize newer threads. We’d call this an unfair scheduler. I talk about fairness in a TLA+ context here.

Most system properties are safety properties, but all systems need at least some liveness properties. Without them there’s no reason to have a system in the first place!

There is no equivalent to invariants in liveness properties; they are always defined over entire state traces.

Other properties

Safety and liveness properties cover a great deal of things we care about. But what about a property like “if I roll a die, I might get a 6”? This is neither safety nor liveness.⁴

I talked about systems as “anything with changing state”. There’s different formal models of what we mean by “changing” and “state”, which can represent different properties. Safety and liveness come from the Linear Temporal Logic model, which can’t represent “is this possible”. Other formalisms can, but they have to make tradeoffs.

“Is this possible” is a reachability property. Like safety and liveness, there are various classes of reachability properties. In the below state machine, state P is reachable from at least one state, while state Q is reachable from every initial state. Neither are reachable from every possible state.

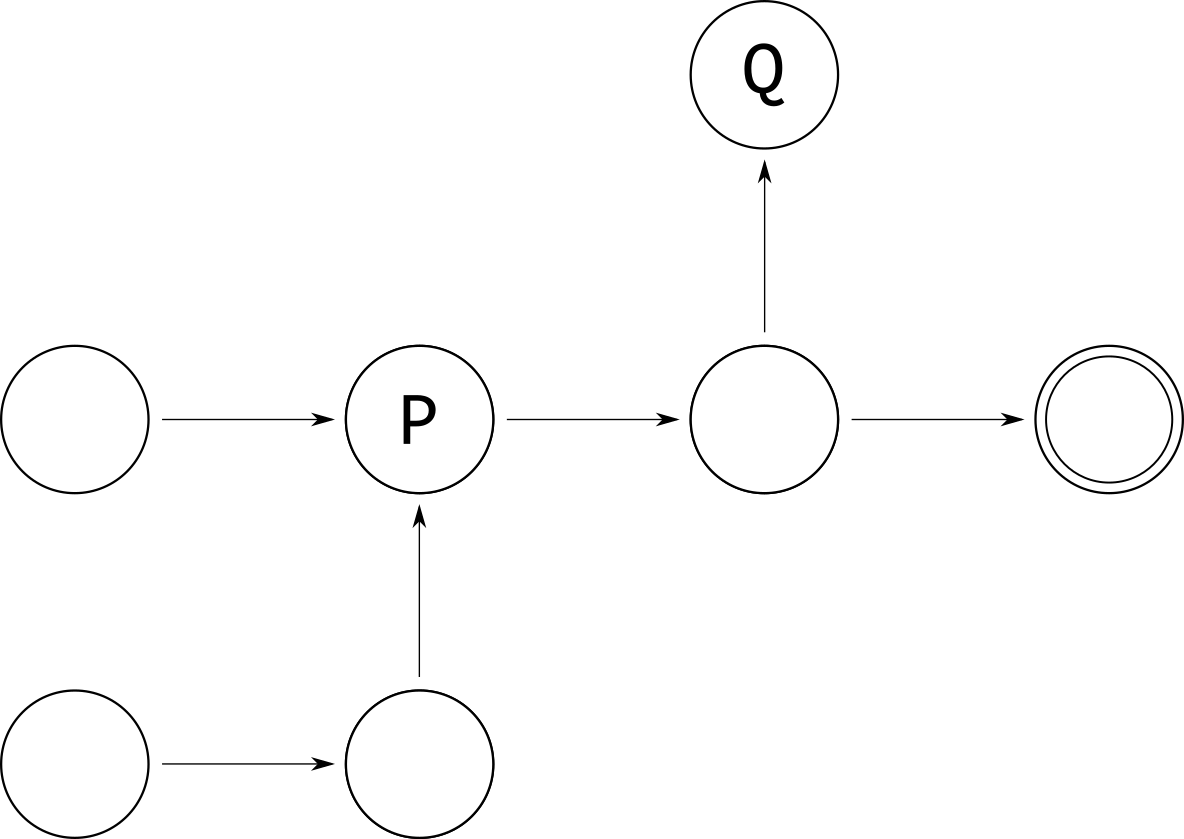
Reachability appears more often in hardware and low-level code. No matter what your computer is doing, the “off” state should always be reachable. Even if most behaviors never actually enter the off state, they’re never permanently prevented from entering it. Otherwise people can’t shut down their computer.

Some other kinds of properties:

• Probabilistic properties: Do 99% of requests complete within 100 milliseconds?
• Optimization properties: Does this algorithm output the minimal cost solution?
• Hyperproperties): Does the algorithm hide internal information from outside observers?⁵
• Superproperties: Does the code still work even if the dependencies change?

Some of these properties can be rewritten as safety or liveness properties, but doing so is difficult and you’re often better off using a specification language dedicated to them.

Takeaways

Even if you’re not doing formal methods, safety and liveness are useful mental models. What properties of the system need to never happen, and what must always happen? What design tradeoffs do you need to make to guarantee those properties, and which ones are not worth making?

If you want to explicitly model the safety and liveness properties of your system, I’d recommend starting with a tool like TLA+, which lets automatically check if your system design maintains your properties. I recently wrote a full, free resource for learning TLA+. I also consult and teach corporate workshops.

Thanks to Lorin Hochstein, Jay Parlar, and Lars Hupel for feedback.